Bölme İşlemi
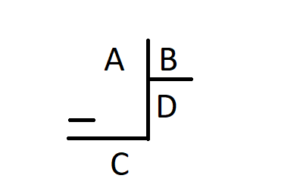
A: Bölünen
B: Bölen
D: Bölüm
C: Kalan
Bölme işleminde A= D . B + C Bölünen sayı bölen ve bölüm çarpımının C ile toplamına eşittir.
C < B Kalan Bölümden küçüktür.
2 il Bölünebilme
Birler basamağında 0, 2, 4, 6, 8 olan sayılar 2 ile kalansız (tam) bölünebilir. İki ile kalansız bölünebilen sayılara çift sayılar denir.
Örnek
*106, 1024, 3338 gibi sayılar 2 ile tam bölünür.
*105, 1027, 3339 gibi sayıların 2 ile bölümünden kalan 1’dir.
3 ile Bölünebilme
3 ile bölünebilmede, rakamların sayı değerleri toplamı 3 veya 3’ün katı olan sayılar 3 ile tam bölünmektedir. Buradan bir sayının 3 ile bölümünden kalan, rakamları toplamının 3 ile bölümünden kalana eşittir mantığı ortaya çıkmaktadır.
Örnek
*627 = 6+2+7=15 Burada 15, 3 ile tam bölünebilmektedir ve kalan 0’dır. Dolayısıyla 627 sayısı da 3 ile tam bölünmektedir.
*329= 3+2+9=14 Burada ise 14’ün 3’e bölümünden kalan 2’dir ve 329 sayısının da 3 ile bölümünden kalan 2’dir deriz.
4 ile Bölünebilme
Son iki basamağının oluşturduğu sayı 00 veya 4’ün katı olan sayılar 4 ile kalansız (tam) bölünebilir.
Örnek
*120, 312, 2000 sayıları 4’e tam bölünebilirler. 2345, 142, 215 sayıları 4’e tam bölünemez.
* 871A sayısı 4 ile kalansız bölünebiliyorsa A yerine gelebilecek rakamların toplamı kaçtır?
4 ile kalansız bölünüyorsa son iki basamağı: 12 ve 16 olabilir. A yerine yazılabilecek rakamların toplamı: 2 + 6 = 8’dir.
Bir sayının 4 ile bölümünden kalanı, son iki basamağındaki rakamların oluşturduğu sayının 4 ile bölümünden kalanına eşittir.
5 ile Bölünebilme
Son rakamı 0 veya 5 olan sayıların hepsi 5 ile tam bölünmektedir.
Örnek
*95, 480, 2635 gibi sayıların son hanesi 0 ya da 5’ten oluştuğu için 5 ile tam bölünmektedir.
8 ile Bölünebilme
Bir sayının son üç rakamı 000 ya da 8’in katı ise bu sayı 8 ile tam bölünür. Bir sayının 8 ile bölümünden kalan, sayının son üç basamağının 8 ile bölümünden kalana eşittir.
Örnek
*1000, 29000, 6048 gibi sayıların son 3 hanesi 000 ya da 8’e bölünebilir olduğundan bu sayılar da 8’e tam bölünür.
9 ile Bölünebilme
Rakamları toplamı 9’un katı olan sayılar 9 ile kalansız (tam) bölünebilir.
Örnek
*5436 sayısı 9 ile tam bölünebilir, çünkü bu sayının rakamları toplamı: 5 + 4 + 3 + 6 = 18’dir.
*2021 sayısı 9 ile tam bölünemez, çünkü bu sayının rakamları toplamı: 2 + 0 + 2 + 1 = 5’tir.
Bir sayının 9 ile bölümünden kalanı, sayının rakamları toplamının 9 ile bölümünden kalanına eşittir.
10 ile Bölünebilme
Son rakamı 0 olan tüm sayılar 10 ile tam bölünür. Bir sayının 10 ile bölümünden kalan ise birler basamağındaki rakamdır
Örnek
*180,2030 gibi sayılar 10 ile tam bölünür.
*1923 sayısının 10 ile bölümünden kalanı son rakamı olduğu gibi 3’tür.
11 ile Bölünebilme
abcdef gibi bir sayının 11 ile bölümünden kalanı bulmak için sayının birler basamağından başlayarak “+” ve “−” işaretleri sırayla yazılır ve aşağıdaki işlemler yapılır.
a b c d e f → (b + d + f) − (a + c + e) işleminin sonucu bulunur.
− + − + − +
Eğer sonuç 0 veya 11’in katı çıkarsa (…, −22, −11, 0, 11, 22, …) bu sayı 11’e kalansız (tam) bölünebilir.
Örnek
*49 676 ve 708 785 sayılarının 11’e tam bölünüp bölünmediğini inceleyelim.
4 9 6 7 6 → (4 + 6 + 6) − (9 + 7) = 0
+ − + − +
Sonuç 0 olduğu için bu sayı 11’e tam bölünür.
*7 0 8 7 8 5 → (0 + 7 + 5) − (7 + 8 + 8) = −11
− + − + − +
Sonuç −11 olduğu için bu sayı 11’e tam bölünür.
